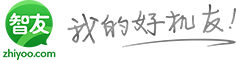袁新意的最新论文在数学界引起了广泛关注。该论文在预印阶段便获得了引用,并在学术会议上受到热议。这一成果的影响力显著,其背后的创新突破备受期待。

袁新意前期成果回顾
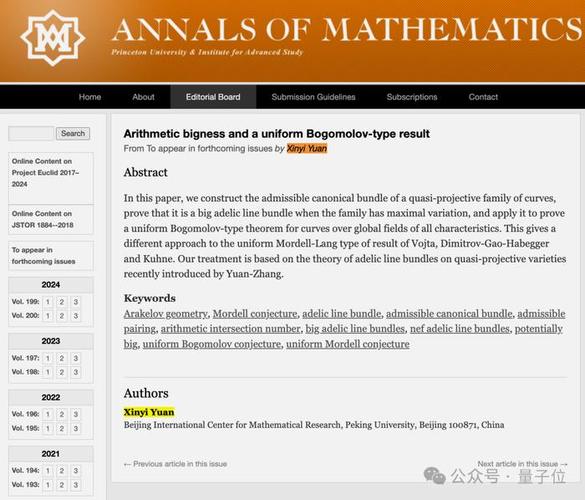
2021年,袁新意与谢俊逸的合作为几何Bogomolov猜想的全面验证提供了实证。这一成就极为重要,使袁新意再次受到广泛关注。在此之前,他在Arakelov几何等多个学术领域已取得显著成绩。比如,在哥伦比亚大学攻读博士学位期间,他与张伟展开了合作,并同张寿武共同取得了相关的研究成果。
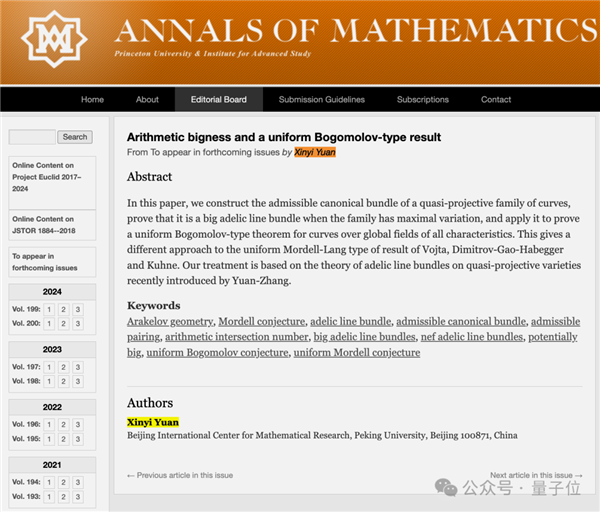
2021年,他在曲线模空间成功建立了算术典范线丛,并对其正性进行了验证,此过程引入了新颖的几何证明方法。这些成就充分体现了他在数学研究领域的卓越实力。
新论文研究内容

该论文在预印阶段即引起广泛关注,原因在于其采用了新颖的研究方法,例如对Uniform Bogomolov问题的转化等。这些方法为相关领域的研究带来了新的视角和工具。依托张寿武的理论,作者的研究工作实现了新的突破。然而,新论文相较于以往,具体在哪些方面具有更显著的开创性细节,尚需进一步深入研究。


该论文在袁新意关于算术几何与丢番图几何的研究基础上进行了扩展。其成果有望为后续研究提供指引。
早期合作回顾

2004年,张伟加入哥伦比亚大学,与袁新意共同成为张寿武的弟子。这段合作成为了一段佳话。他们首先攻克了库达拉猜想中模性问题的相关成果,这些成果构成了张伟的博士论文核心内容。他们深入研究了公式,并将其推广至全实域。


在志村簇上复乘点的高度,他们取得了新的成就。他们构建的Waldspurger公式,在算术代数几何领域的模拟效果超越了之前的公式。北大数院2000级这两位学子的合作成果显著。
袁新意的自身优势

袁新意身为奥数冠军队的一员。他凭借稳健的数学基础,确保了结论的精确性。他的研究涵盖了多个重要领域,对算术几何的整体进步贡献显著。他对各领域知识的深入理解和灵活运用,彰显了他作为一名杰出数学家的才能。


他在与众多数学家合作时表现卓越,这一特质不仅使他独树一帜,而且为其新论文的深入研究打下了坚实基础。
归国任教情况
2020年,袁新意毅然选择重返故乡,加盟母校北京大学,担任教授一职,至今仍在该校任教。他的回归对北大数学领域的研究与学科进步起到了积极的促进作用。在母校的讲台上,他致力于知识的传承,激发学生的研究热情。同时,国内环境也为他提供了进一步推动学术研究的助力。

他的回国从事教学,为我国数学领域注入了新的活力,有望吸引更多人才投身于数学研究工作。
有待解决的难题
Bogomolov猜想的阶段性研究已取得成果,然而,算术几何领域仍面临众多挑战,例如ABC猜想和BSD猜想等。这些难题构成了数学界面前的重大攻关课题。

袁新意及其团队未来是否会调整研究方向至这些问题领域,这无疑将成为数学界关注的中心议题。随着研究进程的持续,我们不禁要问,这些新论文的发现将如何为未来的研究提供启示和指导?
读者们,请问您觉得袁新意能否成功解决算术几何领域尚未破解的挑战?欢迎点赞、转发和发表您的看法。