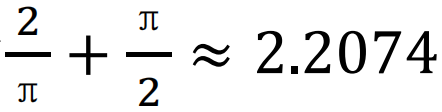
自半个多世纪前起,数学家们便被一个看似简单的沙发移动问题所困扰。这个难题至今仍旧对人类智慧的极限形成挑战。我们接下来将对这个神秘问题的核心进行细致探究。
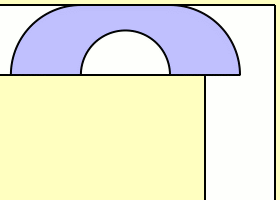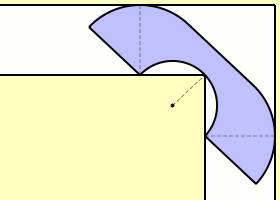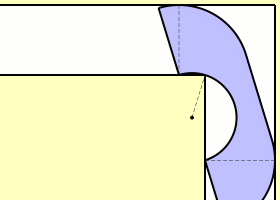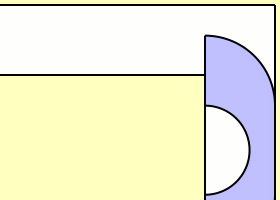
杰弗的改进与突破
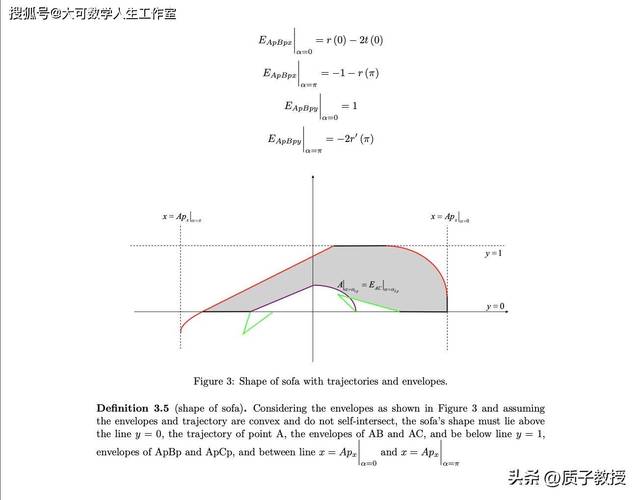
1992年,美国数学家约瑟夫·杰弗开始研究移动沙发问题。他采用哈默斯利设计的“沙发”作为基础,进行了详尽的探究。在此基础上,他提出了一种新方案,该方案由18条光滑曲线构成。经过精确计算,这一方案的最大面积达到了2.2195。这一成果提升了问题解的下限,并为后续研究提供了新的路径。

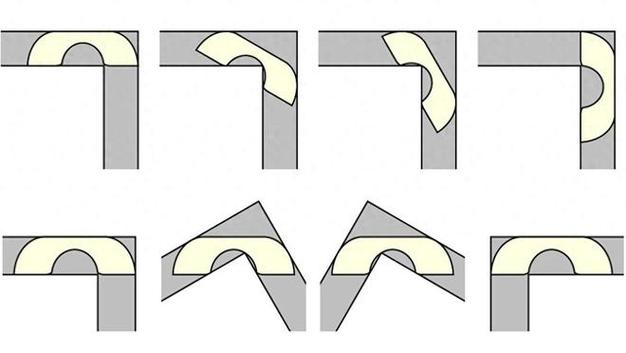
该创新设计颠覆了传统观念,使得对移动沙发的理解发生了根本性的变化。杰弗凭借卓越的数学天赋,在研究领域留下了深刻的印记。众多学者纷纷追随其研究方法,持续深化对该领域的探索。
吉布斯的惊人发现

2014年,菲利普·吉布斯,一名业余数学爱好者,运用计算机手段发现了一种独特的形状。他开发了一种理想的沙发设计方案,并通过细致的对比分析,发现该沙发与约瑟夫·杰弗所设计的“Gerver沙发”极为相似。此外,他还对两者的面积进行了精确计算,结果显示在八位有效数字上完全一致。

数学界对此发现反响强烈,普遍观点认为杰弗提出的“沙发”模型有望成为解决移动沙发问题的有效方案。然而,由于科学研究的严谨要求,这一看法在数学界尚未获得官方认可。众多未解之谜依然亟待解决。
卡鲁斯和罗米奇的成果
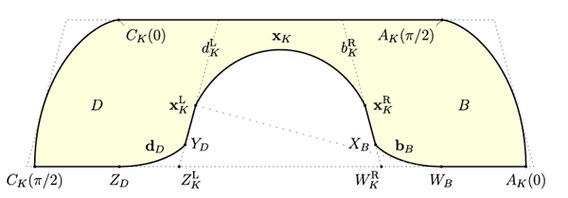
2018年,Yoav Kallus与Dan Romik开展了一项创新性研究。该研究聚焦于走廊,通过调整走廊的转向角度,力求提升交叉区域的连接效率。随后,他们运用计算机技术,成功将“沙发”的阈值降低至2.37。
该成果意义重大,对“移动沙发问题”的理想解区间进行了精确的界定,具体范围为2.2195至2.37。这一界定为后续研究提供了明确的方向,激励了众多数学家进行深入研究。
问题难解之缘由

“移动沙发问题”表面看似不复杂,然而为何数学家们仍对其感到困扰?约瑟夫·杰弗曾提出一个接近最佳的方法,但验证其是否为最优化解的过程相当复杂。这主要是因为,在二维空间中,沙发的形态变化丰富,必须排除所有可能的更优形态。
该方案可能涉及多种形状各异、结构复杂且不规则的多边形。需对每一种可能的形状进行深入分析,并对其面积及移动性进行精确评估。然而,这一研究涉及的计算量极其巨大,几乎无法对所有可能性进行详尽覆盖。此外,这类缺乏规律性且多变性的形状在几何学中本身就较为复杂,难以找到适用于所有情况的通用解法。
新技术应用的限制

自21世纪初以来,计算机技术的迅猛进步为“移动沙发问题”的研究提供了新的机遇。在数学界,普遍运用计算机辅助设计以及运动轨迹模拟技术,这些方法有助于揭示“沙发”的潜在形态,从而显著提高了研究工作的效率。

近期,尽管机器学习领域备受瞩目,但在解决相关问题方面遭遇了显著挑战。数学优化领域亟需兼具高可解释性和精确性的解决方案。然而,由于机器学习模型具有“黑箱”性质,它们仅能提供答案,却无法展示解题过程,这限制了其在直接解决问题上的应用。
跨学科研究的曙光

“移动沙发问题”横跨多个学术领域,包括几何学、优化理论和计算几何等。目前,这一领域的研究正逐步趋向于跨学科合作,致力于探索有效的解决方案。白真允首次对沙发形状的最优限制提出了观点,同时强调沙发的形状可以通过旋转走廊的交点来界定。
在运动过程中,他验证了“沙发”关键点轨迹不相互交错,构成了平面上的纯闭合图形。这一发现确保了面积计算的精确性。众多来自各行各业的专业人士正齐心协力,有望为这个持续半个多世纪的问题提供突破性的解决策略。
针对“移动沙发”相关事务的处理速度,您有何见解?欢迎在评论区分享您的观点。同时,恳请您对本文给予点赞,并协助转发。